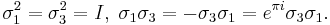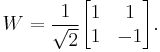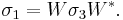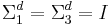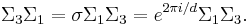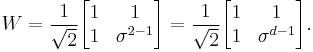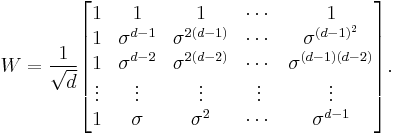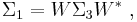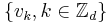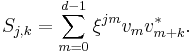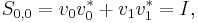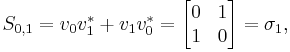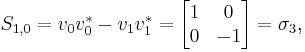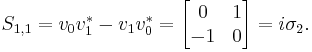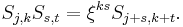Generalizations of Pauli matrices
In mathematics and physics, in particular quantum information, the term generalized Pauli matrices refers to families of matrices which generalize the (linear algebraic) properties of the Pauli matrices. In this article we give a few classes of such matrices.
Contents |
Generalized Gell-Mann matrices
Construction
Let 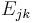 be the matrix with 1 in the
be the matrix with 1 in the 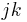 -th entry and 0 elsewhere. Consider the space of
-th entry and 0 elsewhere. Consider the space of 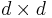 complex matrices,
complex matrices, 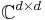 , for a fixed d. Define the following matrices
, for a fixed d. Define the following matrices
- For
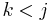 ,
, 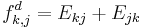 .
.
- For
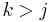 ,
, 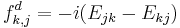 .
.
- Let
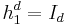 , the identity matrix.
, the identity matrix.
- For
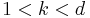 ,
, 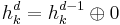 .
.
- For
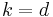 ,
, 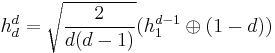 .
.
The collection of matrices defined above are called the generalized Gell-Mann matrices, in dimension d. The symbol  above means matrix direct sum.
above means matrix direct sum.
Properties
The generalized Gell-Mann matrices are Hermitian and traceless by construction, just like the Pauli matrices. One can also check that they are orthogonal in the Hilbert-Schmidt inner product on 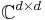 . By the dimension count, we see that they span the vector space of
. By the dimension count, we see that they span the vector space of 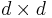 complex matrices.
complex matrices.
In dimensions 2 and 3, the above construction recovers the Pauli and Gell-Mann matrices, respectively.
A non-Hermitian generalization of Pauli matrices
The Pauli matrices 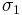 and
and 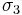 satisfy the following:
satisfy the following:
The so-called Walsh-Hadamard matrix is
Like the Pauli matrices, W is both Hermitian and unitary. 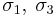 and W satisfy the relation
and W satisfy the relation
The goal now is to extend above to higher dimensions.
Construction
Fix the dimension d as before. Let 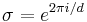 , a root of unity. Since
, a root of unity. Since 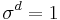 and
and 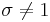 , we have
, we have
Now define, with J. J. Sylvester (1882) the shift matrix[1]
and the clock matrix,
These matrices generalize 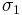 and
and 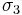 respectively. Note that the tracelessness of the two Pauli matrices is preserved, but not Hermiticity in dimensions higher than two. Since Pauli matrices describe Quaternions, Sylvester dubbed the higher-dimensional analogs "nonions", "sedenions", etc. These two matrices are also the cornerstone of quantum mechanical dynamics in finite-dimensional vector spaces[2] [3] as formulated by Hermann Weyl, and find routine applications in numerous areas of mathematical physics. The clock matrix amounts to the exponential of position in a "clock" of d hours, and the shift matrix is just the translation operator in that cyclic vector space, so the exponential of the momentum.
respectively. Note that the tracelessness of the two Pauli matrices is preserved, but not Hermiticity in dimensions higher than two. Since Pauli matrices describe Quaternions, Sylvester dubbed the higher-dimensional analogs "nonions", "sedenions", etc. These two matrices are also the cornerstone of quantum mechanical dynamics in finite-dimensional vector spaces[2] [3] as formulated by Hermann Weyl, and find routine applications in numerous areas of mathematical physics. The clock matrix amounts to the exponential of position in a "clock" of d hours, and the shift matrix is just the translation operator in that cyclic vector space, so the exponential of the momentum.
The following relations echo those of the Pauli matrices:
and
On the other hand, to generalize the Walsh-Hadamard matrix W, note
Define the following matrix, still denoted by W as a slight abuse of notation:
It is evident that W is no longer Hermitian, but is still unitary. Direct calculation yields
which is the desired result.
When 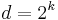 ,
, 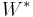 is precisely the matrix of the discrete Fourier transform, converting position coordinates to momentum coordinates and vice-versa
is precisely the matrix of the discrete Fourier transform, converting position coordinates to momentum coordinates and vice-versa
A unitary generalization of the Pauli matrices
As noted above, the Pauli matrices are both Hermitian and unitary. The unitarity has not been extended by generalizations given so far. We now give a generalization which does so. (Although Hermiticity will no longer hold, in general.)
Construction
Again fix the dimension d. Let 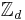 be the abelian ring of integers modulo d. All indices in the subsequent discussion will be considered elements of this group, that is, all operations are to be understood modulo d. The set
be the abelian ring of integers modulo d. All indices in the subsequent discussion will be considered elements of this group, that is, all operations are to be understood modulo d. The set
denotes the standard orthonormal basis for the d-dimensional Hilbert space. Put 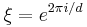 . The generalization we are interested in is defined by
. The generalization we are interested in is defined by
Clearly the family specified by above consists of unitary matrices.
To see that they indeed generalize the Pauli matrices, in some sense, we compute for 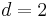 , where
, where 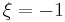 :
:
and
Properties
The set 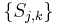 are called generalized spin matrices.[4] Some properties of
are called generalized spin matrices.[4] Some properties of 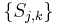 are:
are:
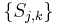 form an orthogonal set in
form an orthogonal set in 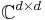 in the Hilbert-Schmidt sense. Therefore by the dimension count, they span the set of
in the Hilbert-Schmidt sense. Therefore by the dimension count, they span the set of 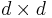 matrices. (Recall this is also true for
matrices. (Recall this is also true for 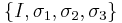 in dimension 2.)
in dimension 2.)
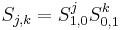 .
.
See also
Notes
- ^ Sylvester, J. J., (1882), Johns Hopkins University Circulars I: 241-242; ibid II (1883) 46; ibid III (1884) 7-9. Summarized in The Collected Mathematics Papers of James Joseph Sylvester (Cambridge University Press, 1909) v III
- ^ Weyl, H., "Quantenmechanik und Gruppentheorie", Zeitschrift für Physik, 46 (1927) pp. 1–46, doi:10.1007/BF02055756.
- ^ Weyl, H., The Theory of Groups and Quantum Mechanics (Dover, New York, 1931)
- ^ Pittenger, A. (2004). "Mutually unbiased bases, generalized spin matrices and separability". Linear Algebra and its Applications 390: 255–278. doi:10.1016/j.laa.2004.04.025.